17. The positive integers $m$, $n$ and $p$ satisfy the equation $3m+\dfrac{3}{n+\frac{1}{p}}=17 %speech% 3,m + 3 divided by  n+1 divided by p=17.$

‍

What is the value of $p$?

18. Two circles $C_1$ and $C_2$ have their centres at the point (3,4) and touch a third circle, $C_3$. The centre of $C_3$ is at the point (0,0) and its radius is 2.

What is the sum of the radii of the two circles $C_1$ and $C_2$?

‍

19. The letters $p$, $q$, $r$, $s$ and $t$ represent different positive single-digit numbers such that $p$−$q$ = $r$ and $r$ − $s$ = $t$.

‍

How many different values could $t$ have?

20. The real numbers $x$ and $y$ satisfy the equations $4^y=\dfrac{1}{8(\sqrt2)^{x+2}}$ and $4^y=\dfrac{1}{8(\sqrt2)^{x+2}}$.

What is the value of $5^{x+y}$?

‍

21. When written out in full, the number $(10^{2020}+2020)^2 %speech% 10^{2020}+2020)^2$ has 4041 digits.

What is the sum of the digits of this 4041-digit number?

22. A square with perimeter 4 cm can be cut into two congruent right-angled triangles and two congruent trapezia as shown in the first diagram in such a way that the four pieces can be rearranged to form the rectangle shown in the second diagram.

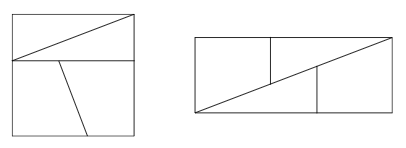
What is the perimeter, in centimetres, of this rectangle?

23. A function $f$ satisfies $y^3f(x)=x^3f(y)$ and $f(3)\not=0.$

What is the value of $\dfrac{f(20)-f(2)}{f(3)}$ ?

24. In the diagram shown, $M$ is the mid-point of $PQ$. The line $PS$ bisects $\angle{RPQ}$ and intersects $RQ$ at $S$. The line $ST$ is parallel to $PR$ and intersects $PQ$ at $T$.

The length of $PQ$ is 12 and the length of $MT$ is 1. The angle $SQT$ is $120^\circ$.

What is the length of $SQ$ ?

25. A regular $m$-gon, a regular $n$-gon and a regular $p$-gon share a vertex and pairwise share edges, as shown in the diagram.

What is the largest possible value of $p$ ?