17. Amy, Beth and Claire each has some sweets. Amy gives one third of her sweets to Beth. Beth gives one third of all the sweets she now has to Claire. Then Claire gives one third of all the sweets she now has to Amy. All the girls end up having the same number of sweets.
Claire begins with 40 sweets. How many sweets does Beth have originally?
18. The arithmetic mean, A, of any two positive numbers 𝑥 and 𝙮 is defined to be A = $\frac{1}{2}$ (𝑥 + 𝙮 ) and their geometric mean, G, is defined to be G = $\sqrt𝑥𝙮$.
For two particular values 𝑥 and y, with 𝑥 > 𝙮, the ratio A : G = 5 : 4. For these values of 𝑥 and 𝙮, what is the ratio 𝑥 : 𝙮?
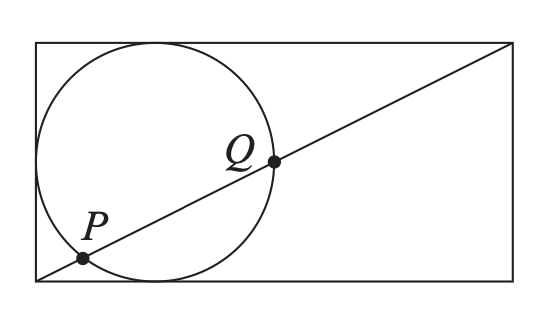
19. The diagram shows a circle of radius 1 touching three sides of a 2 × 4 rectangle. A diagonal of the rectangle intersects the circle at P and Q, as shown.
What is the length of the chord PQ?
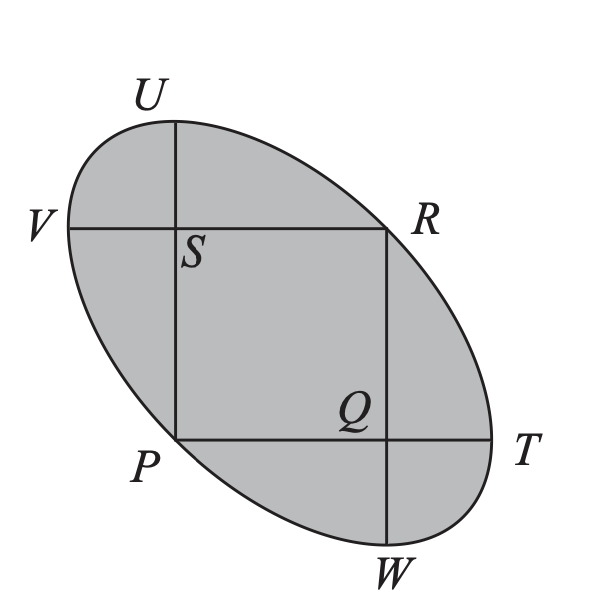
20. The diagram shows a square PQRS with edges of length 1, and four arcs, each of which is a quarter of a circle. ArcTRU has centre P; arc VPW has centre R; arc UV has centre S; and arc WT has centre Q.
What is the length of the perimeter of the shaded region?
21. How many pairs (𝑥 ,𝙮) of postivie integers satisfy the equation $4^x$ = $y^2$ + 15?
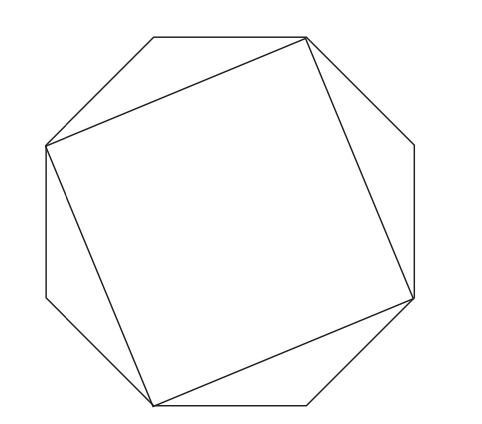
22. The diagram shows a regular octagon and a square formed by drawing four diagonals of the octagon. The edges of the square have length 1.
What is the area of the octagon?
23. The parabola with equation 𝙮 = 𝑥² is reflected in the line with equation 𝙮 = 𝑥 + 2.
Which of the following is the equation of the reflected parabola?
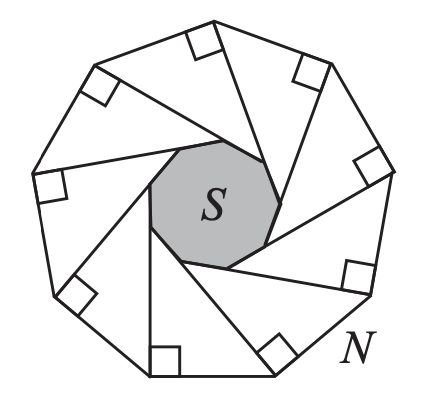
25. The diagram shows a regular nonagon N. Moving clockwise around N, at each vertex a line segment is drawn perpendicular to the preceding edge. This produces a smaller nonagon S, shown shaded.
What fraction of the area of N is the area of S?