17. In 1770, Joseph-Louis Lagrange proved that every positive integer can be written as the sum of four squares.

For example, $13=0^2+0^2+2^2+3^2$

How many of the first $15$ positive integers can be written as the sum of three squares?

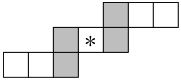
18. Each of the numbers $1$ to $9$ is to be placed in a different cell of the grid shown so that the sum of the three numbers in each row is $15$.

Also, the sum of the two numbers in each shaded column is to be $15$.

How many choices are there for the number to be placed in the central cell indicated by * ?

19. In my class, everyone studies French or German, but not both languages.

One third of the girls and the same number of boys study German.

Twice as many boys as girls study French.

Which of these could be the total number of boys and girls in my class?

20. Each of the four shapes shown below has been made from four unit cubes.

For each shape, Max takes eight copies of the shape and tries to fit them together to make a $2\times4\times4$ cuboid.

How many of the shapes can be used to make a cuboid of that size in this way?

‍

21. Some fish, some dogs and some children are swimming in a bay.

There are $40$ legs in total, twice as many heads as tails and more dogs than fish.

How many fish are in the bay?

22. The diagram shows four congruent rectangles, each of perimeter $20$cm, surrounding a square

of area $44$cm².

What is the area, in cm², of each rectangle?

23. Four different positive integers $p,q,r,s$ satisfy the equation $(9-p)(9-q)(9-r)(9-s)=9$.

What is the value of $p+q+r+s$?

24 .In the diagram shown, $PQ=PR=QS$. Line segments $P⁢R$ and $Q⁢S$ are perpendicular to each other.

What is the sum of $\angle{PRQ}$ and $\angle{PSQ}$ ?

25. I choose four different integers. When I add all the pairs of these numbers in turn, the totals that I obtain are $23, 26, 29, 32 \text{ and } 35$, with one of these totals being repeated.
What is the largest of the four integers?

‍